Main page
About us
Sliding Bearings Consulting
Advertising Opportunities

SubsTech’s sister website Smooth Sliding provides independent engineering consulting services that help you to solve engine bearing related issues: failures, material selection, geometry design and optimization of hydrodynamic conditions.
Smooth Sliding is an engineering consulting company run by Dr. Dmitri Kopeliovich:
- VP R&D of King Engine Bearings.
- World leading expert (32 years of experience) in design, technology and materials for Engine bearings in applications such as automotive, renewable energy, aviation, racing and others.
- Founder and owner of SubsTech (Substances & Technologies) – a leading professional website on Materials Science and Engineering.
- Author of numerous scientific and engineering publications and patents.
- Founder and owner of Smooth Sliding.
For further information and for requesting consulting services please visit our sister website Smooth Sliding.
to Metals
to Engine bearings
Hydrodynamic lubrication theory
Dr. Dmitri Kopeliovich
A theoretical analysis of hydrodynamic lubrication was carried out by Osborne Reynolds.
The equations resulted from the analysis has served a basis for designing hydrodynamically lubricated bearings.
The following assumptions were made by Reynolds in the analysis:
- The lubricating fluid is Newtonian - the flow is laminar and the shear stress between the flow layers is proportional to the velocity gradient in the direction perpendicular to the flow (Newton’s law of viscosity):
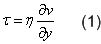
Where:
η – dynamic viscosity of oil,
v – linear velocity of the laminar layer,
y - the axis perpendicular to the flow direction.
- The inertia forces resulted from from the accelerated movement of the flowing lubricant are neglected.
- The lubricating fluid is incompressible.
- The pressure of the fluid p is constant in the direction perpendicular to the laminar flow: dp/dy=0 (assumption of thin lubrication film).
- The viscosity of the fluid is constant throughout the lubrication film.
Consider the equilibrium of a unit volume in the lubricant film.
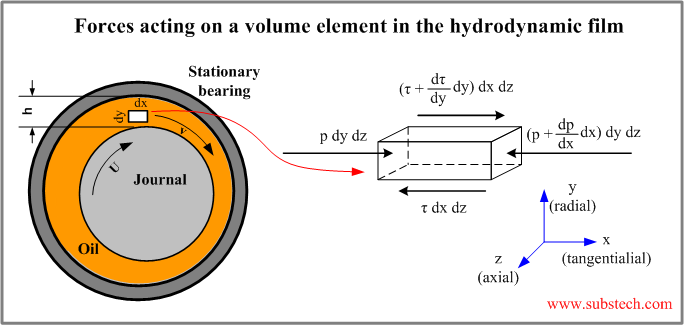
The pressure forces act on the right and the left faces of the unit volume.
The shear forces resulting from the relative motion of the laminar layers act along the upper and the lower faces of the unit volume.
Assuming that there is no flow in z direction the equation of the equilibrium of the forces in the direction of the flow is as follows:
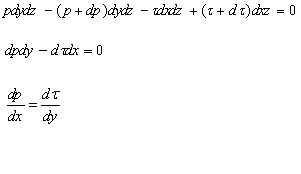
Substitution of τ from Newton’s law of viscosity (1) results in:
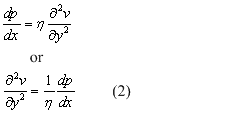
The velocity function is obtained by integrating the equation (2) with respect to y:
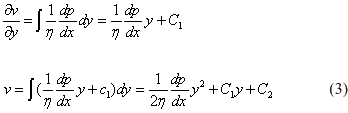
The constants of integration C1 and C2 may be determined from the boundary conditions:
v=U when y=0, then C2=U
v=0 when y=h, then:
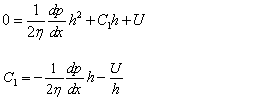
Substituting C1 and C2 in (3) we obtain:
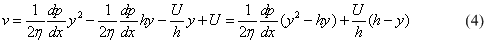
The total flow of the lubricant is:
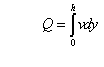
Substituting v from (4) we get:
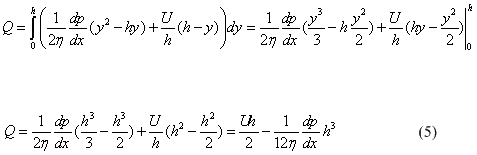
According to the assumption about incompressibility of the lubricant the flow Q does not change in x direction:
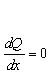
Differentiating the equation (5) with respect x results in:
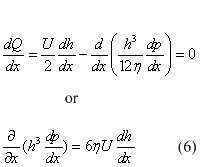
This is Reynolds equation for one dimensional flow.
It can be used with the assumption of no flow in z direction (bearings with infinite length).
If the flow in z direction is taken into account (bearings with side leakage of the lubricating fluid) then the analysis results in Reynolds equation for two dimensional flow:
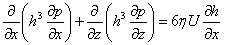
Where:
h – local oil film thickness,
η – dynamic viscosity of oil,
p – local oil film pressure,
U – linear velocity of journal,
x - circumferential direction.
z - longitudinal direction.
Close form solution of Reynolds equation can not be obtained therefore finite elements method is used to solve it.
Analytical solutions of Reynolds equation exist only for certain assumptions:
- Sommerfeld Solution
The equation is solved with the assumption that there is no lubricant flow in the axial direction (infinitely long bearing assumption).
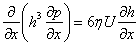
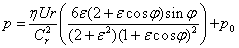
- Ocvirk Solution
Ocvirk solution for infinitely short bearing assumption neglects circumferential pressure gradients (first term of Reynolds equation).
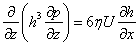
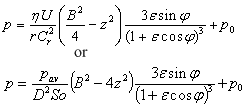
Where:
Cr – radial clearance Cr = (D-Dj)/2,
r – bearing radius,
Dj - journal diameter,
ε - eccentricity ratio ε = e/Cr
e - absolute bearing eccentricity,
B – bearing length,
p0 - cavitation pressure,
So - Sommerfeld number (see below).
So = F Ψ²/(DBωη)
Where:
F – bearing load,
Ψ – relative bearing clearance Ψ = (D-Dj)/D,
D – bearing diameter,
ω – angular speed of journal.
Sommerfeld and Ocvirk solutions are applicable only in the region of positive pressure.
to top
Related internal links
to Metals
to Engine bearings


